cjtore.blogg.se - Priority queue min heap

#Priority queue min heap full#

Move the last child node of the last level to root.To remove/delete a root node in a Max Heap, you: The key here is, whatever operation being carried out on a Max Heap, the heap property must be maintained. These steps can also be followed when inserting new elements into a heap. Repeat until the largest element is at the root parent nodes (then you can say that the heap property holds).Swap nodes if the value of the parent is less than that of either child (to the left or right).Compare the value of the child node with the parent node.

Create a new node at the beginning (root) of the heap.

This means that the key at the parent node is always greater than the key at both child nodes. So, we can call Heapify on the root to make the tree a heap again.Elements in a max heap follow the max heap property. Now the root is equal to the last element of the heap, we delete the last element easily by reducing the size of the heap by 1.ĭoing this, we have disturbed the heap property of the root but we have not touched any of its children, so they are still heaps. Firstly, we store the value of the root in a variable to return it later from the function and then we just make the root equal to the last element of the heap. So, we have to return and delete the root of a heap. This is like the pop of a queue, we return the element as well as delete it from the heap. Returning an element from an array is a constant time taking process, so it is a $\Theta(1)$ process. So, we just need to return the element at the root of the heap. We know that the maximum (or minimum) element of a priority queue is at the root of the max-heap (or min-heap).

#Priority queue min heap full#

However, full code in C, Java and Python is given for both max-priority and min-priority queues at the last of this article.Īs stated earlier, we are going to use a heap for the priority queue. The Pseudo codes given below are for a max-priority queue. Let's learn to code these operations to make a priority queue. But we may also face a situation in which we need to change the key of an element, so Increase/Decrease key is used to do that. With these operations, we have fulfilled most of our demand of a priority queue i.e., to insert data into the queue and take data from the queue. The entire point of the priority queue is to get the data according to the key of the data and the Maximum/Minimum and Extract Maximum/Minimum does this for us. So, inserting a new data must go in a place according to the specified order. Increase/Decrease key → To increase or decrease key of any element in the queue.Ī priority queue stores its data in a specific order according to the keys of the elements.

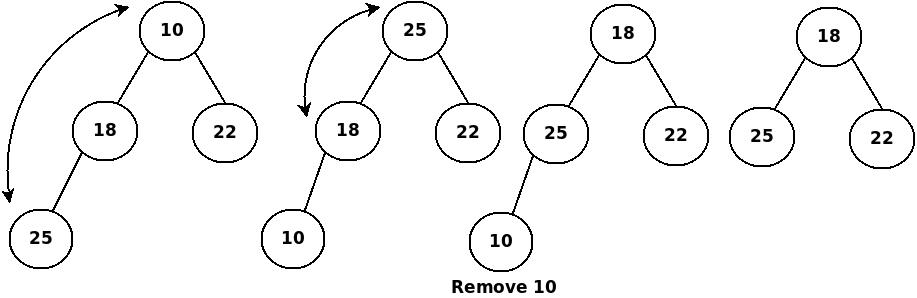
Extract Maximum/Minimum → To remove and return the maximum and the minimum element from the max-priority queue and min-priority queue respectively.Ĥ. Maximum/Minimum → To get the maximum and the minimum element from the max-priority queue and min-priority queue respectively.ģ. Insert → To insert a new element in the queue.Ģ.

There are mainly 4 operations we want from a priority queue:ġ. We use a max-heap for a max-priority queue and a min-heap for a min-priority queue. Heaps are great for implementing a priority queue because of the largest and smallest element at the root of the tree for a max-heap and a min-heap respectively. It is also used in scheduling processes for a computer, etc. Priority queues are used in many algorithms like Huffman Codes, Prim's algorithm, etc. Thus, a max-priority queue returns the element with maximum key first whereas, a min-priority queue returns the element with the smallest key first. Priority queue is a type of queue in which every element has a key associated to it and the queue returns the element according to these keys, unlike the traditional queue which works on first come first serve basis.